曲线参数空间
September 27, 2013
关于计算几何学,人们通常对曲线参数有误解。因为Nurbs曲线的数学十分的难懂-大部分知识肯定超过高中数学,所以很难去解释控制点坐标、控制点权重、曲线阶数和节点向量是如何共同作用,这样只会让Nurbs曲线参数化更难以理解。我自己对Nurbs数学的掌握也一般般,所以我想如果使用更简单的曲线类型开始这个讨论,对每个参与者来说都更好。
但是在讨论问题之前,首先应该确定一些基本规则,定义什么样的形状被我们认可为‘曲线’:
- 曲线是一个有限的、一维的物体,存在于具有任意维度数的某个空间中。本文只关注2维和3维空间,因为大家对这2个空间比较熟悉。
- 每条曲线必须有两个端点。不能多,不能少。
- 如果端点重合,曲线被认为是闭合的。
- 曲线内部没有缺口,因为那会导致端点多于2个。
- 曲线不能有分支,排除端点与曲线内部某点重合的情况。
可以想像任意曲线像长条状橡胶糖那样,可以对它们拉伸、弯曲、扭转和打结,你就得到了一堆变形的橡胶糖而已。注意上面对曲线的定义和通常数学上的定义不一样。数学定义范围更广更精确。
因为所有曲线都有2个端点(就叫它们起点和终点,这样好区分),我们可以说:曲线存在于一个数值区间或域内。这个域由两个极限间所有的数字组成(包含两个极限在内) 1
曲线区间/域
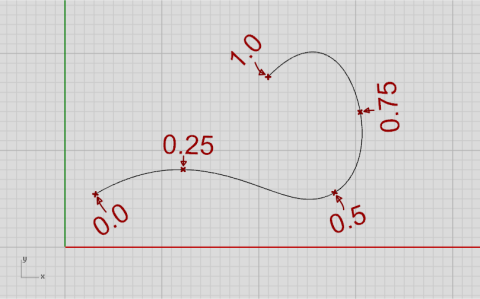
上图展示了一个域为[0.0, 1.0]的二维曲线。0代表曲线的起点,1代表终点,任意位于区间[0, 1]内的数值代表曲线间的某一点。这里选择0和1因为它们都是整数,但是任意非0长度的域都是合法的。比如 [-π, +π]或 [1000000.0, 1000000.1]。 2
让人困惑的第一件事是:曲线的域和曲线的长度几乎没有关系。你可以改变曲线的域,但是并不影响曲线的外形或尺寸;也可以改变曲线的形状,但是同样不影响曲线的域。更坏的是,属于域的某个部分的曲线数量与该子域的大小几乎没有关系。从上图可以看到,在子域[0.25, 0.5]内的曲线明显比在 [0.0, 0.25]的多。
所以到底什么是曲线参数,或者说曲线参数化到底是什么意思?所有数学曲线都是通过一系列函数定义的。一个大家都知道的非常著名的函数就是:正弦函数,就是生成正弦波的函数。因为这是一条2维曲线,需要两个函数来表示:
- x = t
- y = Sin(t)
第一个等式展示沿X轴上曲线的行为,第二个等式定义沿Y轴的行为。变量t在这里被称为参数。曲线参数化是我们用来描述曲线参数特性的词语,以区别于描述几何特性的用语。参数化包含比如域和密度这些特性,它们定义了曲线任意位置的‘速度’。如果你还把曲线相像成可拉伸的条状橡胶糖,那么曲线的‘速度’就是和橡胶糖厚度相似的特性。你拉伸曲线越厉害,橡胶糖就会变得更细,曲线速度就越高。
如果想知道任意给定参数t曲线的位置,只要把t代入两个公式,就可以得到当t时的坐标。如果想知道同样参数t时的正切向量,就不是计算等式本身了,需要计算它们的一阶导数;如果想知道曲率,计算二阶导数,等等等等。 3
如果我们计算一系列等间距参数t的等式值,就会得到下面这样的图:
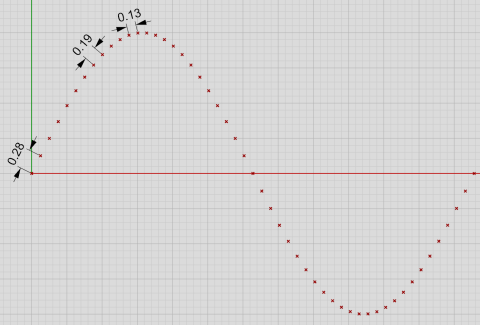
正统波参数
所在红点在水平方向上距离是相等的,但是在垂直方向上的距离随着正弦波函数变化。基于这点,相邻两点间的实际距离总是不同的。当曲线以最大速度向上时,这个距离有0.28这么大;当曲线逼近顶点时,这个距离只有0.13这么小了。这是参数‘密度’在曲线不同部分差异的绝佳例子。
基于我们定义曲线的方式(使用正弦波函数),对于某个特定参数,计算曲线点非常容易与快速。然而对于某个给定长度,计算曲线点会非常困难与耗时。从曲线起点沿着曲线x单位找到对应的参数曲线点,数学计算量是惊人的。这就是为什么在Rhino和Grasshopper里,几乎所有的曲线方法接收曲线参数,而不是曲线长度。
我们继续沿着Nurbs曲线参数的演进,去看看在更复杂的几何图形上它们表现如何。现在看一个阶数=2,有3个等间距、共线控制点的Nurbs曲线:
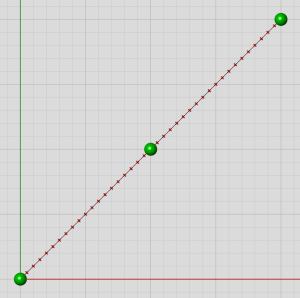
线性参数
看起来沿着曲线的参数密度是一个常量。这是因为控制点完全对称的结果,任意区域将会造成参数拉伸的效果被对称的同一个点抵消了。但是不要认为每条有等间距控制点的线性Nurbs曲线都像示例中那样匀称。只要引入了任意额外的复杂性,要达到一致的参数密度都会变得非常困难。把中间控制点向上靠,看会发生什么变化:
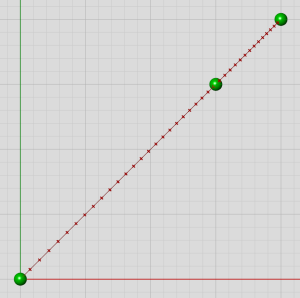
非线性参数
控制点的移动导致了曲线一端的拉伸和另一端的压缩。曲线的外形和之前完全相同,但是它已经不再是原来那条曲线了。控制点的位置并不是决定参数密度的唯一因素。结点向量(本文不讨论)和控制点权重都扮演着重要的角色。比如下图中,中间控制点的权重是10.0,而两边的控制点权重为1.0:
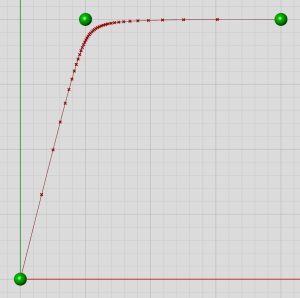
参数权重
如果沿着曲线随机选一点,有可能你选到的点在一条直线上。然而如果你选一个随机参数,有可能会遇到一个急转弯。因此,根据您的迎角,这条曲线要么看起来非常弯曲,要么看起来很直。当面对高阶Nurbs曲线时(3阶和5阶都很常见),即使控制点权重很小,在曲线的末端参数也往往会出现明显的拉伸。 4
到现在为止我们只说了正弦波和Nurbs曲线,那么相似类型的直线、多重直线、圆和弧线是什么情况呢?对于这些类型的曲线,实际上很容易以参数密度恒定的方式定义它们。当以等间距 t对弧线进行采样时,步长将是恒定的。而且不仅仅是距离是恒定的,一阶、二阶、三阶等等导数也是一致的:
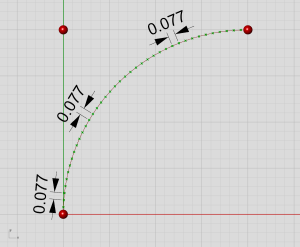
弧线参数化(点击查看动画)
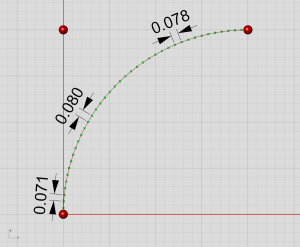
然而,把这些曲线转换为等价的Nurbs曲线时(比如在Rhino里打开控制曲线的控制点),所有这些美妙的特性都会消逝。和前面的例子一样,Nurbs曲线和原来弧线的外面完全一致,但是由于现在参数密度是变量,曲线上的导数已经不再一致:
弧线参数化(点击查看动画)
最后,再回顾一下:
- 不要混淆曲线参数和曲线长度
- 不要设想曲线域为一个特定值,它有可能是任意值。
- 不要以为以恒定步长沿曲线域移动意味着也在以恒定的速度沿着曲线移动。
- 具有相同形状的曲线可能具有截然不同的参数化实现。