8.4 线段与多重直线

你会很开心的认识到，(多重)直线本质上来说和点列表是一样的。唯一的区别是我们把代表直线的点视为序列，而不是随机集合，这样我们就能在序列间画线了。这里有些小问题很容易导致翻车，我们最好现在就解决它。

在openNURBS™即Rhino内部有几种方法表现多重直线。有一个专门的多重直线类，只是一个简单的有序点列表。它没有额外开销数据，因此这是最简单的情况。当把常规Nurbs 曲线的阶数设置为 1 时，它们也可以表现为多重直线。此外，多重直线也可以由线段、多重直线、阶数为1的Nurbs曲线或上述曲线的组合构成。如果使用_Polyline命令创建多重直线，您将获得一个完美的多重直线对象，如左侧的"对象属性详细信息"对话框所示：

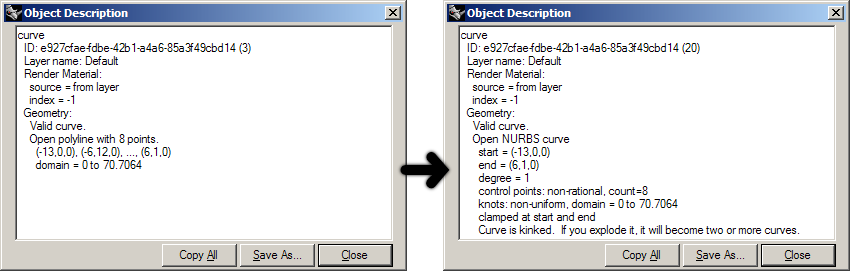
该对话框声明"具有 8 个点的开放多重直线"。但是，当我们拖动控制点时，Rhino会自动将任何曲线转换为Nurbs曲线，如右图所示。它现在是一个阶数为1的开放曲线。从几何角度来看，这两条曲线是相同的。从程序的角度来看，它们不是。目前，我们只会处理"合适"的多重直线;顺序坐标列表。为了便于澄清，我添加了两个示例函数，用于对折线点列表执行基本运算。

计算基于点数组的多重直线段的长度：

def PolylineLength(arrVertices):
    PolylineLength = 0.0
    for i in range(0,len(arrVertices)-1):
        PolylineLength = PolylineLength + rs.Distance(arrVertices[i], arrVertices[i+1])
    return PolylineLength

下面这段不是原文，自己练习，直接选取一条线段并计算长度。不需要提供点数组。

def pline_length():
    crv_id = rs.GetObject('select a polyline', 4, True, True)
    if not rs.IsPolyline(crv_id):
        print('Not a polyline')
        return

    pline_len = 0.0
    arr_vertices = rs.PolylineVertices(crv_id)
    for i in range(0, len(arr_vertices) - 1):
        pline_len += rs.Distance(arr_vertices[i], arr_vertices[i + 1])
    return pline_len

通过在所有现有顶点之间添加额外的顶点来细分多重直线：

import rhinoscriptsyntax as rs

def SubDividePolyline(arrV):
    arrSubD = []

    for i in range(0, len(arrV)-1):
        # copy the original vertex location
        arrSubD.append(arrV[i])
        # compute the average of the current vertex and the next one
        arrSubD.append([(arrV[i][0] + arrV[i+1][0]) / 2.0, 
                        (arrV[i][1] + arrV[i+1][1]) / 2.0, 
                        (arrV[i][2] + arrV[i+1][2]) / 2.0])

    # copy the last vertex (this is skipped by the loop)
    arrSubD.append(arrV[len(arrV)-1])
    return arrSubD

# For testing this func, you can add below code
# gid = rs.GetObject('Select polyline')
# points = SubDividePolyline(rs.PolylineVertices(gid))
# for p in points:
#     rs.AddPoint(p)

原文勘误

第3行：函数声明后没有冒号:

第15行：最后一点的索引是[len(arrV)-1]

第10行: 计算平均点括号使用混乱，本文已更正并运行通过

如您所知，两点之间的最短路径是一条直线。对于我们所有的空间定义，从\(R^1\)到\(R^N\)都是如此。但是，\(R^2\)空间中的最短路径不一定是\(R^3\)空间中的最短路径。如果我们想用\(R^2\)中的直线连接曲面上的两个点，我们需要做的就是通过曲面[u，v]空间绘制一条线性路线。(由于我们只能向 Rhino 添加使用 3D 世界坐标的曲线，因此我们需要相当数量的样点来给人以平滑度的印象。)上图中的红色粗曲线是连接 [A] 和 [B] 的\(R^2\)参数空间中的最短路径。我们可以清楚地看到，这绝对不是\(R^3\)空间中最短的路径。

暂时还没有高科技，但要为下一个例子做好准备......

我们可以清楚地看到这一点，因为我们已经习惯了\(R^3\)空间中发生的事情，这就是为什么整个\(R^2\) / \(R^3\)的事情从一开始就如此彻底地违反直觉。绿点虚线是\(R^3\)空间中的实际最短路径，它仍然尊从曲面的限制（即它可以投影到曲面上而不会丢失任何信息）。以下函数用于创建红色曲线;它创建一条多重直线，表示曲面参数空间中从 [A] 到 [B] 的最短路径：

import rhinoscriptsyntax as rs

def getr2pathonsurface(surface_id, segments, prompt1, prompt2):
    start_point = rs.GetPointOnSurface(surface_id, prompt1)
    if not start_point: return

    end_point = rs.GetPointOnSurface(surface_id, prompt2)
    if not end_point: return

    if rs.Distance(start_point, end_point)==0.0: return

    uva = rs.SurfaceClosestPoint(surface_id, start_point)
    uvb = rs.SurfaceClosestPoint(surface_id, end_point)

    path = []
    for i in range(segments):
        t = i / segments
        u = uva[0] + t*(uvb[0] - uva[0])
        v = uva[1] + t*(uvb[1] - uva[1])
        pt = rs.EvaluateSurface(surface_id, u, v)
        path.append(pt)
    path.append(end_point)
    return path
# For testing this func, you can add below code
# gid = rs.GetObject('Select surface')
# points = getr2pathonsurface(gid, 42, 'Select Point A', 'Select Point B')
# rs.AddInterpCrvOnSrf(gid, points)

行	描述
1	函数接收4个参数：绘制最短路径平面的ID，多重直线的段数，以及选择A、B选择点的两个提示。
1...3	提示用户选在曲面上择A点。如果未选择就跳出程序。
5...6	提示用户选在曲面上择B点。如果未选择就跳出程序。
10...11	投影A和B至曲面以取得\(R^2\)坐标uva 和 uvb。
13	声明保存多重直线所有顶点的列表。
14	因为算法基于分段，我们提前知道多重直线顶点的数量，进而也知道需要对曲面进行的采样次数。
15	t在整个迭代过程中从0.0 增加至 1.0
16...17	使用当前t值在区间uvA至uvB.采样曲面。
18	rs.EvaluateSurface() 接收{u}和{v}值，返回一个3D世界坐标。这是转换\(R^2\)坐标至\(R^3\)坐标的一个友好的方法。

我们要结合以上例子，在Rhino里写一个真正的测量路径程序。整个算法稍显复杂，我会尽我所能在真正写代码前解释清楚它的工作原理。

首先，在\(R^2\)空间生成一条[A]和[B]之间最短路径的多重直线。这是我们的基线。这条线只是粗略的近似线，只有10个分段。使用getr2pathonsurface()函数生成这条线。不幸的是那个程序对闭合曲面并没有作用。在Nurbs曲面章节再细说这个问题。

一旦得到基线，将进入迭代环节。迭代包含2个嵌套循环，我们用2个函数来做这个循环，以免产生太多的嵌套和缩进。除这上面说到的生成近似线函数，我们还需要写4个新函数：

• geodesiccurve() - 测量主程序
• ProjectPolyline() - 投影多重直线
• SmoothPolyline() - 平滑多重直线
• GeodesicFit() - 测地线(最短路径)

主程序 geodesiccurve() 的功能一如继往：收集原始输入数据，尽可能成功的完成程序主要功能。因为我们需要计算曲面上2点间的最短路径，原始输入数据就只包含了曲面ID和带曲面参数空间的2个点数据。寻找最短路径的算法相对来说速度很慢，它不太擅长对对密集多重直线进行重大更改。所以我们只能分批次传送数据。也是基于这个原因我们的初始多重直线(首次传送的数据)只有10段。我们会计算这10个分段的最短路径；然后把生成的多重直线再细分为20段，再计算最短路径；然后再分成40段，继续计算...这样迭代下去直到生成的细分段整体长度变化很小就停止迭代。

ProjectPolyline() 函数确保多重直线顶点的点数组都位于特定曲面之上。为了做到这一点必须把多重直线\(R^3\)坐标投影至曲面之上，然后把投影结果再转换回\(R^3\)空间。这叫‘拉回’。

SmoothPolyline() 会使用多重直线相邻顶点平均这条多重直线。这个函数和前面的例子相似，实现起来会很简单，因为函数处理的不是Nurbs曲线，不需要担心结点、权重、阶数和域会对结果造成影响。

GeodesicFit() 是生成最短路径需要的例程。函数把接收到的多重直线转换成可能的最短路径，不管输入的糟糕和错误程度。解决最短路径使用的算法非常幼稚，比Rhino内置命令_ShortPath慢很多。但是我们算法的也有一个好处，它能处理自交曲面。

算法内在原理和约束橡胶带仿真差不多，唯一的区别是不允许橡胶带离开曲面。内部过程是迭代式的，因此我们可以期望每多进行一次迭代就会比上一次产生更好的结果，迭代效果在接近完美解决方案附近会越来越小。一旦我们觉得效果改进已经可以忽略不计时，就停止迭代退出函数。

为了模拟橡胶带我们需要两个步骤：平滑和投影。首先我们允许橡胶带收缩(在[A]和[B]点间它总是倾向于收缩为直线)。在\(R^3\)空间的收缩意味着多重直线的顶点有可能脱离曲面。必须重新施加影响让顶点重回曲面。这两个操作由函数#2和#3完成。

上图描述了构成最短路径程序的单个迭代的两个步骤。黑色多重直线投影到曲面形成红色多重直线。红色曲线然后平滑化成绿色曲线。请注意实际算法中，这两个步骤是反向进行的：先平滑化，再投影。

从最简单的函数开始:

def projectpolyline(vertices, surface_id):
    polyline = []
    for vertex in vertices:
        pt = rs.BrepClosestPoint(surface_id, vertex)
        if pt: polyline.append(pt[0])
    return polyline

行	描述
1...3	因为只有本程序使用这个函数，我们可以不投影第一个和最后一个点。我们可以安全的假设多重直线是开放的，并且两个端点已经在曲线上了。
4	我们给出多重直线顶点坐标，向Rhino拿到曲面上投影最近点。不使用 rs.SurfaceClosestPoint() 的原因是 BRepClosestPoint() 会把修剪曲面计算在内。通过这个特性我们能得到好处。内置命令 _ShortPath 同样也不考虑修剪曲面的情况。我们当然不会对已经有的轮子有兴趣，我们需要做得更好。
5	如果 BRepClosestPoint() 返回值为Null，那么有地方存在问题。在这种情况下我们不能把顶点投影到曲面，所以最简单的方式是忽略它。出现这种错误时，当然也可以终止整个函数操作，但是我偏向于继续执行，看到最后到底会发生什么。
6	BRepClosestPoint() 函数返回很多信息，不单单只是\(R^2\)坐标。实际上它返回的是一个数据元组，第一个元素是\(R^3\)坐标。这意味着我们不需要自己转换uv坐标到xyz坐标。太好了！直接赋值并继续下一步。

def smoothpolyline(vertices):
    smooth = []
    smooth.append(vertices[0])

    for i in range(1, len(vertices)-1):
        prev = vertices[i-1]
        this = vertices[i]
        next = vertices[i+1]
        pt = (prev+this+next) / 3.0
        smooth.append(pt)
    smooth.append(vertices[len(vertices)-1])
    return smooth

行	描述
1..3 &6..8	因为在整个平滑化过程中我们都需要原始坐标，所以不能直接对整个坐标组进行转换。所以在处理坐标前，我们需要对每个坐标进行一次复制。
9	这里进行的操作是对当前顶点('当前'由参数i定义)在x,y,z坐标方向上进行平均，使用当前坐标本身以及相邻的两个坐标。我们迭代所有内部顶点，同时添加Point3d物体，而不是分别指定x,y,z的值。写子函数不会让代码执行更快，但是这会让程序变得小巧。同时，这也让后面进行调整更容易，因为需要改动的地方不多。

上面提到的难点到了，实际执行寻找最短路径的函数：

def geodesicfit(vertices, surface_id, tolerance):
    length = polylinelength(vertices)
    while True:
        vertices = smoothpolyline(vertices)
        vertices = projectpolyline(vertices, surface_id)
        newlength = polylinelength(vertices)
        if abs(newlength-length)<tolerance: return vertices
        length = newlength

行	描述
1	嗯...看起来不是很垃圾，对吧？你会发现通常很容易说明白的东西到最后写出的代码更多。精密的数学和逻辑结构写起代码来更高效。
2	我们会监控每次迭代过程，一旦发现曲线不再明显变短(‘明显’由参数tolerance定义)，把当前计算的‘中间值’当成‘结果值’并终止程序执行。为了监控这个过程，程序需要记住每次开始迭代前曲线的长度：参数length服务于这个目的。
3	无论在哪里如果你看到不带任何标准跳出条件语句的while True:，就应该提高警惕了。这是一个潜在的无限循环。我已经相当彻底的测试过，它从来没运行超过120次。实验数据从来都不是无懈可击的，从理论上讲，程序可以进入一个在两个解决方案之间跳跃的稳定状态。如果发生了这种情况，循环就永远不会结束，变成死循环。当然如果你觉得需要，欢迎添加跳出条件语句
4...5	算法的主干，调用前面写的2个函数
6	计算新生成多重直线的长度
7	检查是否有必要继续迭代
8	如果需要继续运行，我们现在需要记住这个新的长度作为我们的参考值。

主程序需要解释一下。它执行很多不同任务，让一大堆代码看起来很难理解。可能更好的处理方式是把它分解成更多的小块，但是这个程序已经有7个子函数，我感觉到已经差不多了。记住把问题分解成更小的子问题是组织思维的一个好方式，但是它实际上并不能解决任何问题。你需要寻找一个分割和统一的平衡点。

def geodesiccurve():
    surface_id = rs.GetObject("Select surface for geodesic curve solution", 8, True, True)
    if not surface_id: return

    vertices1 = getr2pathonsurface(surface_id, 10, "Start of geodes curve", "End of geodes curve")
    if not vertices1: return

    tolerance = rs.UnitAbsoluteTolerance() / 10
    length = 1e300
    newlength = 0.0

    while True:
        print("Solving geodesic fit for %d samples" % len(vertices1))
        vertices = geodesicfit(vertices1, surface_id, tolerance)

        newlength = polylinelength(vertices)
        if abs(newlength-length)<tolerance: break
        if len(vertices)>1000: break
        vertices = subdividepolyline(vertices)
        length = newlength

    rs.AddPolyline(vertices)
    print "Geodesic curve added with length: ", newlength

原文勘误

原程序无法运行，原因是变量名混乱。vertices这个变量，有两个不同意义的值使用了这一个变量名。最后可运行的程序在末尾有下载。

行	描述
2...3	选择需要生成最短路径的工作曲面
5...6	声明存储多重直线顶点的变量。因为 getr2pathonsurface() 返回值已经是数组，声明时就不需要使用方括号指示这是一个数组了，前面的例子都是这么干的。
8	程序使用的限值是文档公差的10%
9...12	这个循环也使用长度比较来决定是否继续进行循环。这里不比较多重直线在平滑/投影函数迭代后的长度，而是检测分段/寻找最短路径函数后长度的变化。目的是评估是否值得再继续进行迭代。变量length和newlength和上一页函数的作用一样。
13	在命令行显示信息以通知用户程序的进程。这个程序可能会行动一段时间，所以不要让用户觉得这玩意挂掉了。
14	调用子函数 geodesicfit() 。
16...17	比较长度有无变化，当变化长度小于限值时退出循环
18	安全保障。我可不想生成的曲线太密集了。
19	调用函数 subdividepolyline() 会让多重曲线顶点翻倍。新增点并不在曲面表面，把新生成的多重直线加入文件之前，必须确保至少调用一次函数 geodesicfit() 。
22...23	添加曲线并打印一条曲线长度信息

提供验证过的可运行程序下载 原来用hexo部署在gitee的文件都挂掉了。需要程序重新写。 8.4.py