calculus_with_python

本书来源实际上去gitbook阅读体验会更好，只是有时网速会慢。由于epub格式公式显示全是乱的，就整理了一下输出PDF以便阅读。整理好的PDF下载

关于¶

谨以此书献给我亲爱的家人

Python部分利用到了Numpy,Matplotlib,Sympy等Library。

建议新手安装Enthought的 Canopy Python Distribution ，本书中用到的Library就都满足了。

推荐的函数库调用方法：

import numpy as np

import matplotlib.pyplot as plt

import sympy

第一部分单元微积分¶

函数¶

我们可以将函数(functions) 想象成一台机器$f$，每当我们向机器提供输入$x$，这台机器便会产生输出$f(x)$。

这台机器所能接受的所有输入的集合称为定义域(domain) ，其所有可能输出的集合称为值域(range) 。函数的定义域和值域有着非常重要的意义，如果我们知道一个函数的定义域，便不会将不合适的输入丢给函数；知道函数的值域，便能判断一个值是否可能是这个函数所输出的。

一些函数的例子：

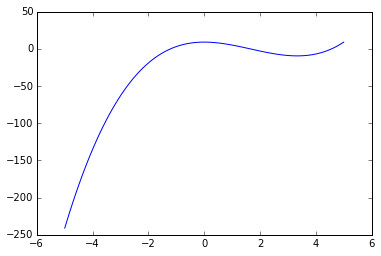
1. 多项式(polynomials) ：

\[f(x)=x^3-5x^2+9\]

因为这是一个三次函数，当$x\to -\infty$ 时 $f(x) \to -\infty$；当$x\to \infty$ 时$f(x)\to \infty$，因此这个函数的定义域和值域都是实属集$\mathbb{R}$。

在Python中，我们这样定义上面这个函数：

def f(x):

    return x**3 - 5*x**2 + 9

函数定义好后，我们可以测试一下其是否正确：

print f(3)
-9

print f(1)
5

读者可以自行计算一下，与Python中我们所定义函数所给出的结果比较一下。

通常，将函数绘制成函数图能够帮助我们理解函数的变化。

import numpy as np

x = np.linspace(-5, 5, num = 100)

y = f(x)

import matplotlib.pyplot as plt

plt.plot(x,y)

2. 指数函数(Exponential Functions) :

\[exp(x)=e^x\]

其定义域为$(-\infty,\infty)$，值域为$(0,\infty)$。在Python中，利用欧拉常数$e$可以如下方式定义指数函数：

def exp(x):

    return np.e**x

print exp(2)
7.3890560989306495

或者可以使用numpy自带的指数函数

print np.e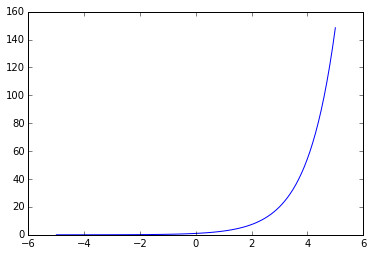xp(2)
7.3890560989306495

指数函数的函数图：

plt.plot(x, exp(x))

注意到，上面的Python定义中，我们只是利用了numpy中现成的欧拉常数$e$,如果没有这个神奇的常数，我们是否就无法定义指数函数了呢？答案是否定的：

def exp2(x):

    sum = 0

    for k in range(100):
        sum += float(x**k)/np.math.factorial(k)

    return sum

print exp(1), exp(2), exp(3)
2.718281828459045 7.38905609893 20.0855369232

print exp2(1), exp2(2), exp2(3)
2.7182818284590455 7.38905609893 20.0855369232

上面定义中的奇妙公式：

\[e^x = \sum_{k = 0}^{\infty}\frac{x^k}{k!}\]

究竟是从何而来，又为何是这样的，将是本书讨论的重点之一。

3. 对数函数(Logarithmic Functions) :

\[log_{e}(x)=ln(x)\]

对数函数是指数函数的反函数，其定义域为$(0,\infty)$，值域$(-\infty,\infty)$。

numpy为我们提供了以$2,e,10$为底的对数函数：

x = np.linspace(0,10,100,endpoint = False)

y1 = np.log2(x)
y2 = np.log(x)
y3 = np.log10(x)

plt.plot(x,y1,'red',x,y2,'yellow',x,y3,'blue')

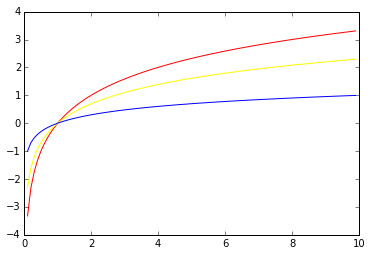
4. 三角函数(Trigonometric Functions) :

周期性是三角函数的特点之一，同时，不同三角函数的值域和定义域也需要我们牢记，下面是Python绘制的一些三角函数的函数图：

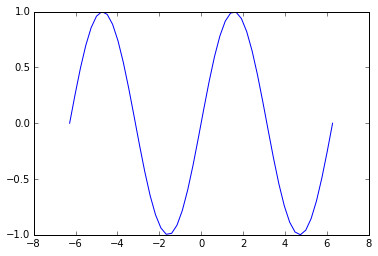
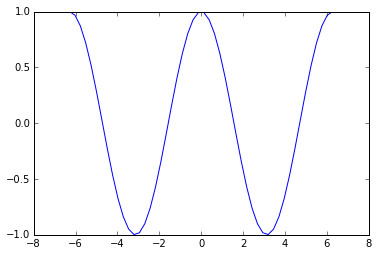
plt.plot(np.linspace(-2*np.pi,2*np.pi),np.sin(np.linspace(-2*np.pi,2*np.pi)))

plt.plot(np.linspace(-2*np.pi,2*np.pi),np.cos(np.linspace(-2*np.pi,2*np.pi)))

这里我们没有给出对数函数和三角函数的数学表达式，没有告诉大家如何在Python中定义自己的对数函数和三角函数。这并不表述我们没法这么做，与指数函数一样，我们会在后面章节为读者揭开这些奇妙函数背后的故事。

复合函数¶

函数的复合（Composition）:

函数$f$和$g$的复合:$f\circ g(x)=f(g(x))$，可以理解为首先将$x$输入给函数$g$获得输出$g(x)$后将其进而输入给函数$f$，最终获得结果$f(g(x))$。

几个函数的复合结果仍是一个函数:接受输入，给出输出。任何函数都可以看成是若干个函数的复合。

$f\circ g(x)$的定义域与$g$的定义域相同，但值域不一定与$f$的值域相同。

例如:$f(x)= x+1,g(x)=x^2,h(x)=x^2+1$,函数$h$可以视为$f$和$g$复合后的结果。$f$的值域为$\mathbb{R}$，但$h$的值域为$(1,\infty)$

在Python中我们可以很直观地对函数进行复合：

def f(x): return x+1
def g(x): return x**2
def h(x): return f(g(x))
x = np.array(range(-10,10))

这里我们使用了Python的list comprehension来计算y

y = np.array([h(i) for i in x])

'bo' 将表示我们会使用蓝色的圆圈绘制点图，而非默认的线图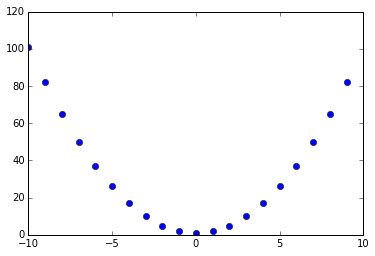

plt.plot(x, y, 'bo')

我们也可以使用Python的lambda函数功能来简明地定义$h$:

h2 = lambda x: f(g(x))
plt.plot(x,h2(x),'rs')

逆函数（Inverse Function）:

给定一个函数$f$，其逆函数$f^{-1}$是一个与$f$进行复合后得到$f\circ f^{-1}(x)=f^{-1} \circ f (x)=x$的特殊函数。

函数与其反函数的函数图一定是关于直线$y=x$对称的：

w = lambda x: x**2
winv = lambda x: sqrt(x)
x = np.linspace(0,2,100)

plt.plot(x, w(x),'b',x,winv(x),'r',x,x,'g-.')

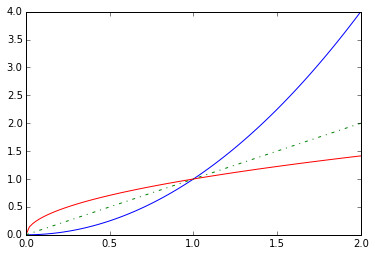
高阶函数（Higher Order Functions）:

我们可以不局限于仅将数值作为函数的输入输出，函数本身也可以作为输入和输出。

def horizontal_shift(f,H): return lambda x: f(x-H)

上面定义的函数$\text{horizontal\_shift}(f,H)$，接受的输入是一个函数$f$个一个实数$H$，而输出是一个新的函数，新函数是将$f$沿着水平方向平移了距离$H$后得到的。

x = np.linspace(-10,10,100)
shifted_g = horizontal_shift(g,2)

plt.plot(x,g(x),'b',x,shifted_g(x),'r')

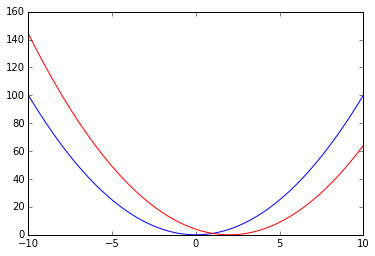
以高阶函数的观点看去，函数的复合便是将两个函数作为输入给复合函数，然后由其产生一个新的函数作为输出。复合函数可以如此定义：

def composite(f,g): return lambda x: f(g(x))

h3 = composite(f,g)

print sum(h(x)==h3(x))==len(x)
# result: True

欧拉公式¶

欧拉公式（Euler's Formula）

在 1.1 中给出了指数函数的多项式形式：

\[e^x =1+\frac{x}{1!}+\frac{x^2}{2!}+\dots = \sum_{k = 0}^{\infty}\frac{x^k}{k!}\]

接下来我不仅暂时不去解释上式是如何来的，而是更丧心病狂地丢给读者两个有关三角函数的类似式子：

\[sin(x) = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots = \sum_{k = 0}^{\infty}{(-1)}^k\frac{x^{(2k+1)}}{(2k+1)!}\]

\[cos(x) = \frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots = \sum_{k = 0}^{\infty}{(-1)}^k\frac{x^{2k}}{(2k)!}\]

在中学数学中，我们都接触过虚数(Imaginary Number) 的概念，这里我们对其来源和意义暂不讨论，只是简单回顾一下其基本的运算规则：

\[i^0=1,\quad i^1=i,\quad i^2=-1,\quad i^3=-i\]

\[i^4=1,\quad i^5=i,\quad i^6=-1,\quad i^7=-i\]

将$ix$带入指数函数的公式中，我们获得：

\[e^{ix}=\frac{(ix)^0}{0!}+\frac{(ix)^1}{1!}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\frac{(ix)^5}{5!}+\frac{(ix)^6}{6!}+\frac{(ix)^7}{7!}+\dots\]

$\qquad =\frac{i^0x^0}{0!}+\frac{i^1x^1}{1!}+\frac{i^2x^2}{2!}+\frac{i^3x^3}{3!}+\frac{i^4x^4}{4!}+\frac{i^5x^5}{5!}+\frac{i^6x^6}{6!}+\frac{i^7x^7}{7!}+\dots$

$\qquad = 1\frac{x^0}{0!}+i\frac{x^1}{1!}-1\frac{x^2}{2!}-i\frac{x^3}{3!}+1\frac{x^4}{4!}+i\frac{x^5}{5!}-1\frac{x^6}{6!}-i\frac{x^7}{7!}+\dots$

$\qquad = (\frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots)+i(\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots)$

$\qquad = cos(x)+isin(x)$

此时，我们便获得了著名的欧拉公式：$e^{ix} = cos(x)+isin(x)$

特别地，令$x=\pi$时：$e^{i\pi}+1=0$

欧拉公式在三角函数、圆周率、虚数以及自然指数之间建立的桥梁，在很多领域都扮演着重要的角色。

如果你对欧拉公式的正确性感到疑惑，不妨在Python中验证一下：

x = np.linspace(-np.pi,np.pi)
# Numpy中虚数用j表示
lhs = e**(1j*x)
rhs = cos(x)+1j*sin(x)
print sum(lhs==rhs)==len(x)
# result: True

我们也可以用sympy来展开$e^x$，得特别注意的是sympy中虚数为I,欧拉常数为E

z = sympy.Symbol('z', real = True)
sympy.expand(sympy.E**(sympy.I*z), complex = True)
#result: I*sin(z) + cos(z)

将函数写成多项式形式有很多的好处，多项式的微分和积分都比较容易。现在你知道了$e^x$,$sin(x)$,$cos(x)$的多项式形式，不妨用其去验证一下中学书本中强行填塞给你这几个公式：

\[\frac{d}{dx}e^x=e^x\]

\[\frac{d}{dx}sin(x)=cos(x)\]

\[\frac{d}{dx}cos(x)=-sin(x)\]

喔，对了，这一章怎能没有图呢？收尾前来一发吧：

for p in e**(1j*x):
    plt.polar([0, angle(p)],[0, abs(p)], marker = 'o')

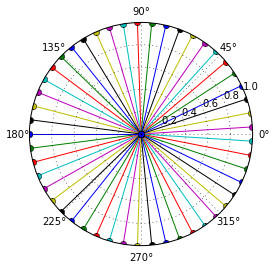
想要理解这张图的几何意义的话，
就请继续学习吧少年

泰勒级数¶

泰勒级数(Taylor Series)

在前几章的预热之后，读者可能会有这样的疑问，是否任何函数都可以写成友善的多项式形式呢？目前为止，我们介绍的$e^x,sin(x),cos(x)$都有其奇妙的多项式形式。这些多项式形式实际为这些函数在$x=0$处展开的泰勒级数。

下面我们给出函数$f(x)$在$x=0$处展开的泰勒级数的定义：

\[f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\dots=\sum_{k=0}^{\infty}\frac{f^{(k)}(0)}{k!}x^k\]

其中：$f^{(k)}(0)$表示函数$f$的$k$次导函数在点$x=0$处的取值。

我们知道对$e^x$无论计算多少次导数结果都是$e^x$（前面也推荐读者自己验证过），即：

$exp'(x)=exp''(x)=exp'''(x)=\dots=exp^{(k)}(x)=exp(x)$

$exp'(0)=exp''(0)=exp'''(0)=\dots=exp^{(k)}(0)=exp(0)=1$

因而，依据上面的定义展开有：

$exp(x)=exp(0)+\frac{exp'(0)}{1!}x+\frac{exp''(0)}{2!}x^2+\frac{exp'''(0)}{3!}x^3+\dots$

$\qquad =1 + \frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots$

$\qquad =\sum_{k=0}^{\infty}\frac{x^k}{k!}$

便得到了在 1.1 中所介绍的公式。

类似地，有兴趣的读者可以尝试用泰勒级数的定义来推导一下$sin(x),cos(x)$关于$x=0$处展开的泰勒级数。

多项式近似(Polynomial Approximantion)

泰勒级数可以把非常复杂的函数转变成无限项的和的形式。通常，我们可以只计算泰勒级数的前几项之和，便能够获得原函数的局部近似了。在做这样的多项式近似时，我们所计算的项越多，则近似的结果越精确。

下面，在Python中试试吧：

import sympy

 # 指定x为符号
x = sympy.Symbol('x')
 # exp为公式
exp = e**x

 # 下面开始求和,就求前21项的和吧

sums = 0

for i in range(20):

 # 求i次导函数

    numerator = exp.diff(x,i)

 # 计算导函数在x=0处的值

    numerator = numerator.evalf(subs={x:0})

    denominator = np.math.factorial(i)

    sums += numerator/denominator*x**i

 # 下面检验一下原始的exp函数和其在x=0处展开的泰勒级数前20项之和的差距

print exp.evalf(subs={x:0})-sums.evalf(subs={x:0})

#    result is 0

xvals = np.linspace(0,20,100)

for xval in xvals:

    plt.plot(xval,exp.evalf(subs={x:xval}),'bo',\

    xval,sums.evalf(subs={x:xval}),'ro')

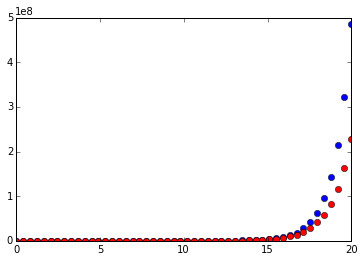
表明指数函数$e^x$在$x=0$处展开的泰勒级数只取前20项的话，在输入值越接近展开点（$x=0$）处的近似效果就越好。

让我们看看采用不同项数所计算出来的近似结果之间的差异：

def polyApprox(func,num_terms):

 # 当我们需要反复做类似的步骤的时候，最好将步骤定义为一个函数

    sums = 0

    for i in range(num_terms):

        numerator = func.diff(x,i)

        numerator = numerator.evalf(subs={x:0})

        denominator = np.math.factorial(i)

        sums += numerator/denominator*x**i

    return sums

sum5 = polyApprox(exp,5)

sum10 = polyApprox(exp,10)

 # 利用sympy我们也可以获得泰勒级数：

sum15 = exp.series(x,0,15).removeO()

xvals = np.linspace(5,10,100)

for xval in xvals:

    plt.plot(xval,exp.evalf(subs={x:xval}),'bo',\

    xval,sum5.evalf(subs={x:xval}),'ro',\

    xval,sum10.evalf(subs={x:xval}),'go',\

    xval,sum15.evalf(subs={x:xval}),'yo')

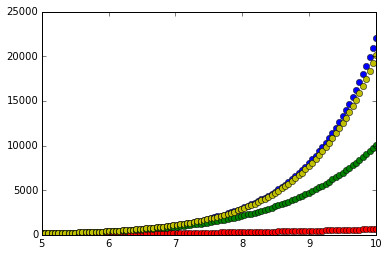
可以明显看出，在输入值远离展开点$x=0$处时，用越多项数获得的近似结果越接近真实值。

展开点（Expansion point）

上面我们获得的泰勒级数都是围绕着$x=0$处获得的，我们发现多项式近似也只在$x=0$处较为准确。如果我们希望在其他位置获得类似的多项式近似，则可以在不同的展开点（例如$x=a$）获得泰勒级数：

\[f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots=\sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(x-a)^k\]

Python中，这也非常容易：

def taylorExpansion(func,var,expPoint,numTerms):

    return func.series(var,expPoint,numTerms)

print taylorExpansion(sympy.tanh(x),x,2,3)

# resulut is :tanh(2) + (x - 2)*(-tanh(2)**2 + 1) + (x - 2)**2*(-tanh(2)\

# + tanh(2)**3) + O((x - 2)**3, (x, 2))

极限¶

极限(Limits)

函数的极限，描述的是输入值在接近一个特定值时函数的表现。

定义：我们若要称函数$f(x)$在$x=a$处的极限为$L$即：$\lim_{x\rightarrow a}f(x)=L$，则需要：

对任意一个$\epsilon > 0$，我们要都能找到一个$\delta >0$使得当$x$的取值满足$0<|x-a|<\delta$时$|f(x)-L|<\epsilon$

本节的重点内容其实是用Python画图...：

f = lambda x: x**2-2*x-6

x = np.linspace(0,5,100)

y = f(x)

plt.plot(x,y,'red')

plt.grid('off')

l = plt.axhline(-8,0,1,linewidth = 2, color = 'black')

l = plt.axvline(0,0,1,linewidth = 2, color = 'black')

l = plt.axhline(y=2,xmin=0,xmax=0.8,linestyle="--")

l = plt.axvline(x=4,ymin=0,ymax=float(5)/9, linestyle = "--")

l = plt.axhline(-6,3.7/5,4.3/5,linewidth = 2, color = 'black')

l = plt.axvline(1,6.0/18,14.0/18,linewidth = 2, color = 'black')

p = plt.axhspan(-2,6,0,(1+sqrt(13))/5,alpha = 0.15, ec = 'none')

p = plt.axvspan((1+sqrt(5)),(1+sqrt(13)),0,1.0/3,alpha = 0.15, ec = 'none')

p = plt.axhspan(f(3.7),f(4.3),0,4.3/5,alpha = 0.3, ec = 'none')

p = plt.axvspan(3.7,4.3,0,(f(3.7)+8)/18,alpha = 0.3, ec = 'none')

plt.axis([0,5,-8,10])

plt.text(0.8,-1,r"$\epsilon$", fontsize = 18)

plt.text(0.8,4,r"$\epsilon$", fontsize = 18)

plt.text(3.75,-7.0,r"$\delta$", fontsize = 18)

plt.text(4.1,-7.0,r"$\delta$", fontsize = 18)

plt.text(3.95,-7.8,r"$a$", fontsize = 18)

plt.text(4.5,8.5,r"$f(x)$", fontsize = 18,color="red")

plt.show()

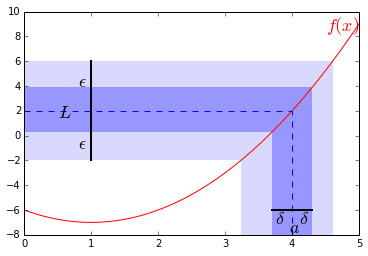
下面尝试用上面的定义来证明$\lim_{x\rightarrow 4}x^2-2x-6=2$:

依据定义，我们需要show的是：对于任意$\epsilon$,能找到一个$\delta$使得：$0<|x-4|<\delta$时有$|f(x)-2|<\epsilon$

注意到$|f(x)-2|=|x^2-2x-6-2|=|(x-4)(x+2)|=|x-4|\cdot|x+2|$，其中我们已经知道$|x-4|<\delta$

依三角不等式有：$|x+2|=|x-4+6|\leq|x-4|+6<\delta+6$

因此$|f(x)-2|=|x-4|\cdot|x+2|<\delta\cdot (\delta+6)$

现在我们只需要找到一个$\delta$满足$\delta\cdot (\delta+6)\leq\epsilon$即可

动用一些中学时候的二元一次方程知识应该很容易证明这样的$\delta >0$是存在的，或者我们只要令$\delta=min(1,\frac{\epsilon}{7})$即可使得$\delta \leq \frac{\epsilon}{7}$且$\delta +6\leq 7$，因而$\delta\cdot (\delta+6)\leq\epsilon$

Python中求该极限方法如下：

x = sympy.Symbol('x',real = True)

y = f(x)

print y.limit(x, 2)
# result is: 2

上图中的函数就是$f(x)=x^2-2x-6$,并且$\epsilon=4,\delta=0.3$

至于趋近于$\infty$的极限定义，就留给读者自己回忆啦。

函数的连续性

极限可以用来判断一个函数是否为连续函数。

当极限$\lim_{x\rightarrow a}f(x)$存在，且$\lim_{x\rightarrow a}f(x)=f(a)$时，称函数$f(x)$在点$x=a$处为连续的。当一个函数在其定义域中任何一点处均连续，则称该函数是连续函数。

泰勒级数用于极限计算

我们在中学课本中一定记忆了常见的极限，以及极限计算的规则，这里我们便不再赘言。泰勒级数也可以用于计算一些形式比较复杂的函数的极限。这里，仅举一例：

$\lim_{x\rightarrow 0}\frac{sin(x)}{x}=\lim_{x\rightarrow 0}{\frac{\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots}{x}}$

$\qquad = \lim_{x\rightarrow 0}{\frac{x(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots)}{x}}$

$\qquad = \lim_{x\rightarrow 0}{1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots}$

$\qquad = 1$

洛必达法则（l'Hopital's rule）

利用泰勒级数来计算极限，有时也会陷入困境，例如：求极限的位置是在我们不知道泰勒展开的位置，或者所求极限是无穷的。通常遇到这些情况我们会使用各种形式的洛必达法则，读者可以自行回顾一下这些情形，这里我们仅尝试说明$\frac{0}{0}$形式的洛必达法则为何成立。

如果$f$和$g$是连续函数，且$\lim_{x\rightarrow a}f(x)=0,\quad \lim_{x\rightarrow a}g(x)=0$。若$\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$ 存在，则：

\[\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}\]

若分子分母同时求导后仍然是$\frac{0}{0}$形式，那么便重复该过程，直至问题解决。运用泰勒级数，我们很容易可以理解洛必达法则为什么会成立:

\[\lim_{x\rightarrow a}{\frac{f(x)}{g(x)}}=\lim_{x\rightarrow a}{\frac{f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{g(a)+\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}\]

\[\qquad = \lim_{x\rightarrow a}{\frac{\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}\]

\[\qquad =\lim_{x\rightarrow a}{\frac{f'(a)+\frac{f''(a)}{2!}(x-a)+\frac{f'''(a)}{3!}(x-a)^2+\dots}{g'(a)+\frac{g''(a)}{2!}(x-a)+\frac{g'''(a)}{3!}(x-a)^2+\dots}}\]

\[\qquad = \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}\]

感兴趣的读者可以自己尝试去验证一下其他形式的洛必达法则。

大O记法¶

大O记法（Big-O Notation）

我们已经见过了很多函数，在比较两个函数时，我们可能会想知道，随着输入值$x$的增长或者减少，两个函数的输出值增长或减少的速度究竟谁快谁慢，哪一个函数最终会远远甩开另一个。

通过绘制函数图，可以获得一些直观的感受：

x = range(1,7)

factorial = [np.math.factorial(i) for i in x]
exponential = [np.e**i for i in x]
polynomial = [i**3 for i in x]
logarithmic = [np.log(i) for i in x]

plt.plot(x,factorial,'black',\
x,exponential, 'blue',\
x,polynomial, 'green',\
x,logarithmic, 'red')

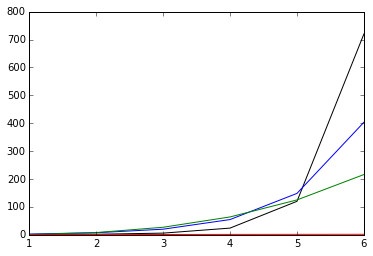
根据上图，当$x\rightarrow \infty$时：$x!> e^x> x^3 > ln(x)$，要想证明的话，可以取极限，例如：$\lim_{x\rightarrow \infty}\frac{e^x}{x^3}=\infty$（用洛必达法则计算），表明$x\rightarrow \infty$时，虽然分子分母都在趋向无限大，但是分子仍然远远凌驾于分母之上，决定了整个表达式的表现。

类似地我们也可以这样看：$\lim_{x\rightarrow \infty}\frac{ln(x)}{x^3}=0$，表明分母将会远远凌驾于分子之上。

from sympy.abc import x

 # sympy中无限infty用oo表示
print ((sympy.E**x)/(x**3)).limit(x,sympy.oo)

# result is: oo
print (sympy.ln(x)/x**3).limit(x,sympy.oo)
# result is 0

为了描述这种随着输入$x\rightarrow \infty$或$x\rightarrow 0$时，函数的表现，我们如下定义大O记法：

若我们称函数$f(x)$在$x\rightarrow 0$时是$O(g(x))$，则需要找到一个常数$C$，对于所有足够小的$x$均有$|f(x)|<C|g(x)|$

若我们称函数$f(x)$在$x\rightarrow \infty$时是$O(g(x))$，则需要找到一个常数$C$，对于所有足够大的$x$均有$|f(x)|<C|g(x)|$

大O记法之所以得此名称，是因为函数的增长速率很多时候被称为函数的阶（Order）。

下面举一例：当$x\rightarrow \infty$时，$x\sqrt{1+x^2}$是$O(x^2)$

先来个直观感受：

xvals = np.linspace(0,100,1000)

f = x*sympy.sqrt(1+x**2)
g = 2*x**2

y1 = [f.evalf(subs={x:xval}) for xval in xvals]
y2 = [g.evalf(subs={x:xval}) for xval in xvals]

plt.plot(xvals[:100],y1[:100],'r',xvals[:100],y2[:100],'b')
plt.plot(xvals,y1,'r',xvals,y2,'b')

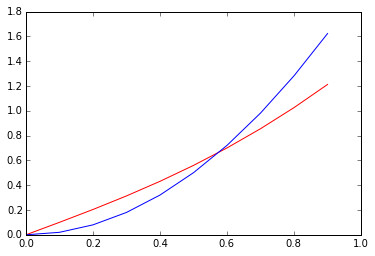
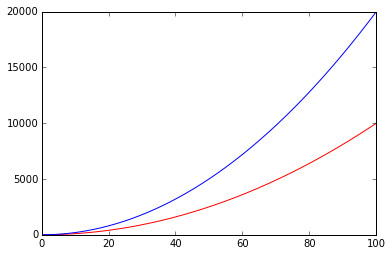
Sympy可以帮助我们分析一个函数的阶：

print sympy.O(f, (x, sympy.oo))
# result is : O(x**2, (x, oo))

计算机学科中使用大O记法，通常是分析当输入数据$\rightarrow \infty$时程序在时间或空间方面的表现。

然而，从上面的介绍，我们知道这个位置可以是$0$，甚至可以是任何有意义的位置。

print sympy.order(f, (x, 0))

# result is : O(x)

误差分析（Error Analysis）

细心的读者可能曾注意到在泰勒级数一节，我们利用Sympy取函数泰勒级数的前几项时，代码是这样的：

exp = e**x

sum15 = exp.series(x,0,15).removeO()

其中 removeO() 的作用是让sympy忽略掉级数展开后的大O表示项，不然的话结果类似如下：

print exp.series(x, 0, 3)

# result is : 1 + 1.0*x + 0.5*x**2 + O(x**3)

这表示从泰勒级数的第4项起，剩余所有项在$x\rightarrow 0$时是$O(x^3)$的。

这表明，当$x\rightarrow 0$时，用$1+x+0.5x^2$来近似$e^x$，我们得到的误差的上限将是$Cx^3$，其中$C$是一个常数。

也就是说大O记法能用来描述我们使用多项式近似时的误差。

另外，大O记法也可以直接参与计算中去，例如我们要计算$cos(x^2)\sqrt{(x)}$在$x\rightarrow 0$时阶$O(x^5)$以内的多项式近似，可以这样：

\[cos(x^2)\sqrt{(x)}=(1-\frac{1}{2}x^4+O(x^6))x^{\frac{1}{2}}\]

$$ = x^{\frac{1}{2}}- \frac{1}{2}x^{\frac{9}{2}} + O(x^{\frac{13}{2}})$$

print (sympy.cos(x**2)*sympy.sqrt(x)).series(x,0,5)

# result is : sqrt(x) - x**(9/2)/2 + O(x**5)

导数¶

切线（Tangent line）

中学介绍导数的时候，通常会举两个例子，其一是几何意上的例子：对函数关于某一点进行求导，得到的是函数该点处切线的斜率。

选中函数图像中某一点，然后不断地将函数图放大，当我们将镜头拉至足够近后便会发现函数图看上去像一条直线，这条直线就是切线。

from sympy.abc import x

 # 函数
f = x**3-2*x-6

 # 在x=6处正切于函数的切线
line = 106*x-438

d1 = np.linspace(2,10,1000)
d2 = np.linspace(4,8,1000)
d3 = np.linspace(5,7,1000)
d4 = np.linspace(5.8,6.2,100)

domains = [d1,d2,d3,d4]

# 画图的函数
def makeplot(f,l,d):

    plt.plot(d,[f.evalf(subs={x:xval}) for xval in d],'b',\

    d,[l.evalf(subs={x:xval}) for xval in d],'r')

    for i in range(len(domains)):
# 绘制包含多个子图的图表
        plt.subplot(2, 2, i+1)
        makeplot(f,line,domains[i])

        plt.show()

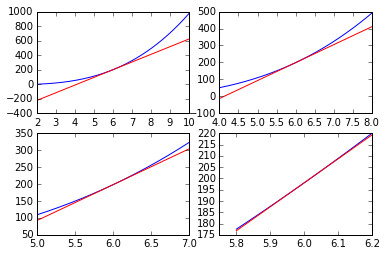
另一个是物理中的例子：对路程的时间函数$s(t)$求导可以得到速度的时间函数$v(t)$，再进一步求导可以得到加速度的时间函数$a(t)$这个理解较好，因为导数真正关心的事是：当我们稍微改变一点函数的输入值时，函数的输出值会有怎样变化。在单元时，导数看上去是曲线的切线斜率，但是到更多元时，就很难有“斜率”这样的直观感受了，但是输出值随着输入值的极小变化而产生的相应变化这样的理解还是成立的。

导数（Derivative）

导数的定义如下：

定义1：

\[f'(a)=\frac{df}{dx}\bigg| {x=a}=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}\]

若该极限不存在，则函数在$x=a$处的导数不存在。

定义2：

\[f'(a)=\frac{df}{dx}\bigg| {x=a}=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]

若该极限不存在，则函数在$x=a$处的导函数不存在。

以上两个定义都是耳熟能详的定义了，就不多说了。

定义3：

函数$f(x)$在$x=a$处的导数$f'(a)$是满足如下条件的常数$C$:

对于在$a$附近输入值的微小变化$h$有，$f(a+h)=f(a)+Ch+O(h^2)$始终成立。也就是说导数$C$是输出值变化中一阶项的系数。

如果难以理解的话，对上式稍加变化，两边同时除以$h$并同时取极限可以得到：

\[\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}=\lim_{h\rightarrow 0}C+O(h)=C\]

便于上面定义2相一致了。

下面举一例，求$cos(x)$在$x=a$处的导数：

$cos(a+h)=cos(a)cos(h)-sin(a)sin(h)$

$\qquad = cos(a)(1+O(h^2))-sin(a)(h+O(h^3))$

$\qquad = cos(a)-sin(a)h +O(h^2)$

因此，$\frac{d}{dx}{cos(x)}\bigg|_{x=a}=-sin(a)$

各位读者可以自行回顾一下求导的规则和技巧，本书中便不进行展开了。

我们可以如下定义自己的求导数的函数：

f = lambda x: x**3-2*x-6

我们设定参数h的默认值，如果调用函数时没有指明参数h的值，便会使用默认值

def derivative(f,h=0.00001):

    return lambda x: float(f(x+h)-f(x))/h

fprime = derivative(f)

print fprime(6)

# result is : 106.000179994

Sympy也提供求导的方法：

from sympy.abc import x

f = x**3-2*x-6

print f.diff()

# result is :3*x**2-2

print f.diff().evalf(subs={x:6})

# result is : 106.0000000000

线性近似（Linear approximation）

依据导数的定义3，我们有：

\[f(a+h)=f(a)+f'(a)h+O(h^2)\]

如果将高阶项丢掉，就获得了$f(a+h)$的线性近似式子：

\[f(a+h)\approx f(a)+f'(a)h\]

举个例子，用线性近似的方法估算$\sqrt{255}$：

\[\sqrt{256-1}\approx \sqrt{256}+\frac{1}{2\sqrt{256}}(-1)\]

\[\qquad = 16 - \frac{1}{32}\]

\[\qquad = 15\frac{31}{32}\]

牛顿迭代法¶

求二次根

各位同学可能遇到过这样的编程题目，要求在不使用$x^{\frac{1}{2}}$或$\sqrt{x}$的前提下，求解$C$的正二次根。

可以用牛顿迭代法解：

def mysqrt(c, x = 1, maxiter = 10, prt_step = False):

for i in range(maxiter):

x = 0.5*(x+ c/x)

if prt_step == True:

# 在输出时，{0}和{1}将被i+1和x所替代

print "After {0} iteration, the root value is updated to {1}".format(i+1,x)

return x

print mysqrt(2,maxiter =4,prt_step = True)

# After 1 iteration, the root value is updated to 1.5
# After 2 iteration, the root value is updated to 1.41666666667
# After 3 iteration, the root value is updated to 1.41421568627
# After 4 iteration, the root value is updated to 1.41421356237

# result : 1.4142135623746899

牛顿迭代法（Newton's Itervative Method）

上面的求正二次根问题，等价于求$f(x)=x^2-c=0$的正根根据上一节介绍的线性近似：

$f(x+h)\approx f(x)+f'(x)h$ 如果$x+h$是$f(x)=0$的一个根，即$f(x+h)=0$，则：

\[h\approx -\frac{f(x)}{f'(x)}\]

\[x+h\approx x - \frac{f(x)}{f'(x)}\]

因此，如果我们对$f(x)=0$的正根有一个初始估计$x_0$，便可以用上面的近似不断获取更加准确的估计值，方法为：

\[x_{n+1} = x_{n} - \frac{f(x n)}{f' {x_n}}\]

将$f(x)=x^2-C$带入上式，便会得到代码中的跟新规则了。

通过绘图我们能进一步了解这个方法（喜闻乐见的绘图时刻又到了！）：

f = lambda x: x**2-2*x-4

l1 = lambda x: 2*x-8

l2 = lambda x: 6*x-20

x = np.linspace(0,5,100)

plt.plot(x,f(x),'black')

plt.plot(x[30:80],l1(x[30:80]),'blue', linestyle = '--')

plt.plot(x[66:],l2(x[66:]),'blue', linestyle = '--')

l = plt.axhline(y=0,xmin=0,xmax=1,color = 'black')

l = plt.axvline(x=2,ymin=2.0/18,ymax=6.0/18, linestyle = '--')

l = plt.axvline(x=4,ymin=6.0/18,ymax=10.0/18, linestyle = '--')

plt.text(1.9,0.5,r"$x_0$", fontsize = 18)

plt.text(3.9,-1.5,r"$x_1$", fontsize = 18)

plt.text(3.1,1.3,r"$x_2$", fontsize = 18)

plt.plot(2,0,marker = 'o', color = 'r' )

plt.plot(2,-4,marker = 'o', color = 'r' )

plt.plot(4,0,marker = 'o', color = 'r' )

plt.plot(4,4,marker = 'o', color = 'r' )

plt.plot(10.0/3,0,marker = 'o', color = 'r' )

plt.show()

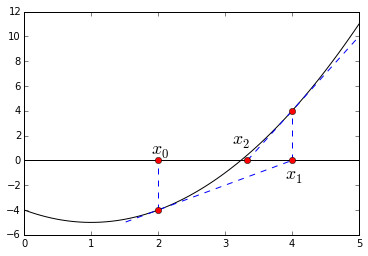
我们要猜$f(x)=x^2-2x-4=0$的解，从$x_0=4$的初始猜测值开始，找到$f(x)$在$x=x_0$处的切线$y=2x-8$，找到其与$y=0$的交点$(4,0)$，将该交点更新为新的猜测的解$x_1=4$，如此循环。

如下定义牛顿迭代法：

def NewTon(f, s = 1, maxiter = 100, prt_step = False):

for i in range(maxiter):

# 相较于f.evalf(subs={x:s}),subs()是更好的将值带入并计算的方法。

s = s - f.subs(x,s)/f.diff().subs(x,s)

if prt_step == True:

print "After {0} iteration, the solution is updated to {1}".format(i+1,s)

return s

from sympy.abc import x

f = x**2-2*x-4

print NewTon(f, s = 2, maxiter = 4, prt_step = True)

# After 1 iteration, the solution is updated to 4
# After 2 iteration, the solution is updated to 10/3
# After 3 iteration, the solution is updated to 68/21
# After 4 iteration, the solution is updated to 3194/987

# 3194/987

Sympy可以帮助我们求解方程，不要教坏小朋友们哦：

sympy.solve(f,x)

# result: [1 + sqrt(5), -sqrt(5) + 1]

优化¶

高阶导数（Higher Derivatives）

高阶导数的递归式定义为：

函数$f(x)$的$n$阶导数$f^{(n)}(x)$（或记为$\frac{d^n}{dx^n}(f)$）为：

\[f^{(n)}(x)=\frac{d}{dx}f^{(n-1)}(x)\]

如果将求导数$\frac{d}{dx}$看作是一个运算符，则相当于反复对运算的结果使用$n$次运算符：

\[{(\frac{d}{dx})}^nf=\frac{d^n}{dx^n}f\]

from sympy.abc import x
from sympy.abc import y

f = x**2*y-2*x*y

# 求关于x的二次导数
print f.diff(x,2)
# result : 2*y

# 等同于反复关于x求两次导数
print f.diff(x).diff(x)
# result : 2*y

# 先求关于x的导数，再求关于y的导数，这个该怎么解读？
print f.diff(x,y)
# result : 2*(x - 1)

优化问题（Optimization Problem）

很多时候，我们用函数来描述我们关心的问题,例如：

plt.figure(1, figsize=(4,4))
plt.axis('off')

plt.axhspan(0,1,0.2,0.8,ec = "none")
plt.axhspan(0.2,0.8,0,0.2,ec = "none")
plt.axhspan(0.2,0.8,0.8,1,ec = "none")

plt.axhline(0.2,0.2,0.8,linewidth = 2, color = 'black')
plt.axvline(0.2,0.17,0.23,linewidth = 2, color = 'black')
plt.axvline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axvline(0.2,0.8,1,linewidth = 2, color = 'black')
plt.axhline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axhline(1,0.17,0.23,linewidth = 2, color = 'black')
plt.text(0.495,0.22,r"$l$", fontsize = 18,color="black")

plt.text(0.1,0.9,r"$\frac{4-l}{2}$", fontsize = 18,color="black")

plt.show()

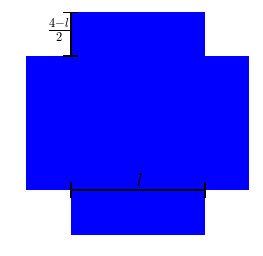
用一张给定边长$4$的正方形纸来折一个没有盖的纸盒，设纸盒的底部边长为$l$，纸盒的高为$\frac{4-l}{2}$，那么纸盒的体积为：

\[V(l)=l^2\frac{4-l}{2}\]

我们会希望知道怎样才能使得纸盒的容积最大，也就是关心在$l>0,4-l>0$,的限制条件下，函数$V(l)$的最大值是多少。

优化问题关心的就是这样的问题，在满足限制条件的前提之下，怎样能够使我们的目标函数最大（或最小）。

l = np.linspace(0,4,100)
V = lambda l: 0.5*l**2*(4-l)

plt.plot(l,V(l))

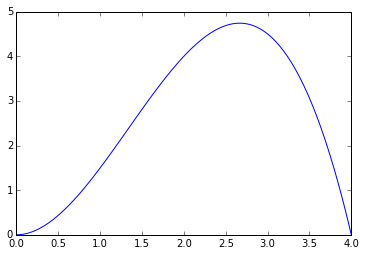
通过观察函数图，不难看出，在$l$的值大约在$2.5$往上去一点的位置处，获得的纸盒的体积最大。

关键点（Critical Points）

通过导数一节，我们知道一个函数在某处的导数所描述的是：当输入值在该位置附近变化时，函数值所发生的相应变化。

因此，如果给定一个函数$f$，如果知道在点$x=a$处函数的导数不为$0$，则在该点出稍微改变函数的输入值，函数值都会变化，这表示函数在该点的函数值即不可能是局部最大值，也不可能是局部最小值。相反，如果函数$f$在点$x=a$处函数的导数为$0$，或者该点出的导数不存在则称这个点就被称为关键点。

要想知道一个$f'(a)=0$的关键点处，函数值$f(a)$是一个局部最大值还是局部最小值，可以使用二次导数测试：

如果$f''(a)>0$，则函数$f$在$a$处的函数值是局部最小值

如果$f''(a)<0$，则函数$f$在$a$处的函数值是局部最大值

如果$f''(a)=0$，则测试无法告诉我们结论

二次导数测试在中学书本中，大多是要求不求甚解地记忆的规则，其实理解起来非常容易。二次导数测试中涉及到函数在某一点处的函数值、一次导数和二次导数，于是想$f(x)$在$x=a$处的泰勒级数：

\[f(x)=f(a)+f'(a)(x-a)+\frac{1}{2}f''(a)(x-a)^2+\dots\]

因为$a$为关键点，$f'(a)=0$，因而：

\[f(x)=f(a)+\frac{1}{2}f''(a)(x-a)^2+O(x^3)\]

表明$f''(a)\neq 0$时，函数$f(x)$在$x=a$附近的表现近似于二次函数，二次项的系数$\frac{1}{2}f''(a)$决定了抛物线的开口朝向，因而决定了函数值在该点是怎样的。

回到之前的求最大盒子体积的优化问题，解法如下：

from sympy.abc import l

V = 0.5*l**2*(4-l)

# 看看一次导函数：

print V.diff(l)

# output is : -0.5*l**2 + 1.0*l*(-l + 4)

# 一次导函数的定义域为(-oo,oo),因此关键点为V'(l)=0的根

cp = sympy.solve(V.diff(l),l)

print cp

# output is: [0.0, 2.66666666666667]

# 找到关键点后，使用二次导数测试：

for p in cp:

print V.diff(l,2).subs(l,p)

# output is: 4, -4

# 因此知道在l=2.666666处时，纸盒的体积最大

线性回归（Linear Regression）

二维平面上有$n$个数据点，$p_i=(x_i,y_i)$，现尝试找到一条经过原点的直线$y = ax$，使得所有数据点到该直线的残差（数据点和回归直线之间的水平距离）的平方和最小。

设定好随机函数种子，确保模拟数据的可重现性

np.random.seed(123)

# 随机生成一些带误差的数据
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res

# 求解回归线的系数
a = sum(x*y)/sum(x**2)

# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red')

for i in range(len(x)):

    plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\

    max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\

    color = 'black')

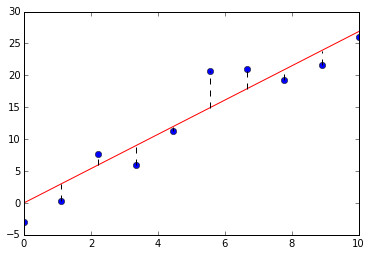
要找到这样一条直线，实际上是一个优化问题：

\[\underset{a}{min}Err(a)=\sum_{i}{(y_i-ax_i)}^2\]

要找出函数$Err(a)$的最小值，首先计算一次导函数：

\[\frac{dErr}{da}=\sum_{i}2(y_i-ax_i)(-x_i)\]

\[\qquad = -2\sum {i}x_iy_i + 2a\sum {i}x_i^2\]

令该函数为$0$，求解出关键点：

\[a = \frac{\sum {i}x_iy_i}{\sum {i}x_i^2}\]

使用二次导数测试：

\[\frac{d^2Err}{da^2}=2\sum ix_i^2>0\]

因此$a = \frac{\sum {i}x iy_i}{\sum {i}x_i^2}$是能够使得函数值最小的输入。

这也是上面Python代码中，求解回归线斜率所用的计算方式。

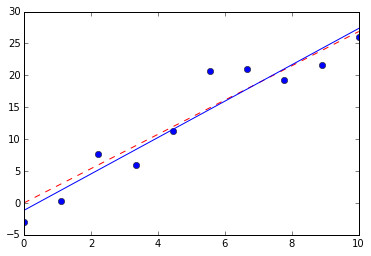
如果我们不限定直线一定经过原点，即公式为$y=ax+b$，则同样还是一个优化问题，只不过涉及的变量变成2个而已：

\[\underset{a}{min}Err(a,b)=\sum_i{(y_i-ax_i-b)}^2\]

这个问题就是多元微积分里所要分析的问题了。

虽然在第二部分才会介绍具体解法，这里先给出一种Python中的求解方法:

slope, intercept = np.polyfit(x,y,1)

plt.plot(x,y,'o')

plt.plot(x,a*x,'red', linestyle = '--')

plt.plot(x,slope*x+intercept, 'blue')

不定积分¶

常微分方程（Ordinary Differential Equations, ODE）

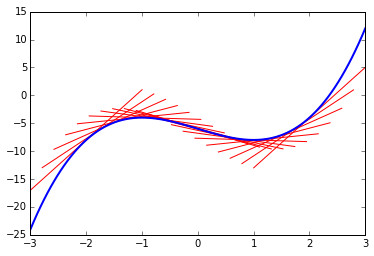
我们观察一辆行驶中的汽车，假设我们发现函数$a(t)$能够很好地描述这辆汽车在各个时刻的加速度，因为对速度的时间函数求导可以得到加速度的时间函数，如果我们希望根据$a(t)$求出$v(t)$，很自然会得出下面这个方程：

\[\frac{dv}{dt}=a(t)\]

如果我们能够找到一个函数$v(t)$满足：$\frac{dv}{dt}=a(t)$，那么$v(t)$就是上面方程的解之一。因为对于常数项求导的结果是0，一旦我们找到了一个$v(t)$是方程的解，那么$\forall C\in\mathbb{R}, v(t)+C$也都是方程的解，因此常微分方程的解是$v(t)+C$这样的一系列函数。

在得出这一系列函数后，我们只需要知道任意一个时刻里汽车行驶的速度，便可以求解出常数项$C$，因而得到最终想求的速度时间函数。

如果我们沿用导数是函数在某个位置的切线斜率的解读去看上面的常微分方程，就像是我们知道了一个函数在各个位置的切线斜率，反过来求这个函数一样。

t = sympy.Symbol('t')
c = sympy.Symbol('c')
domain = np.linspace(-3,3,100)
v = t**3-3*t-6
a = v.diff()

for p in np.linspace(-2,2,20):
    slope = a.subs(t,p)
    intercept = sympy.solve(slope*p+c-v.subs(t,p),c)[0]
    lindomain = np.linspace(p-1,p+1,20)

plt.plot(lindomain,slope*lindomain+intercept,'red',linewidth = 1)
plt.plot(domain,[v.subs(t,i) for i in domain],linewidth = 2)

数学家发明并研究积分的一个重要目的便是为了方便地求解微分方程。

不定积分（Indefinite Integral）

如果我们将求导看作一个高阶函数，输入进一个函数，求导后得到一个新的函数。那么不定积分可以被视为是对应的“反函数”，$F'(x)=f(x)$，则$\int f(x)dx=F(x)+C$。写成类似反函数之间复合的形式有：

\[\int((\frac{d}{dx}F(x))dx)=F(x)+C\]

其中$C$为常数。

积分的规则和技巧，例如换元积分、分部积分等就累给读者去回顾吧，这里仅介绍下Python中的方法。

print a.integrate()

# result is : t**3 - 3*t

print sympy.integrate(sympy.E**t+3*t**2)

# result is : t**3 + exp(t)